Nachhaltige Altersvorsorge – Das Rentendesign „Maximal With-Profit“, Teil 1

In Nachhaltige Altersvorsorge – Neue Konzepte dringend gesucht! wird das schwierige Umfeld für die Altersvorsorge und die Suche nach Modellen mit kollektiver Absicherung statt Garantie beschrieben. Im Folgenden wollen wir eine konkretes Modell vorstellen, das Rentendesign „Maximal with-Profit“. Unsere Darstellung beruht in wesentlichen Teilen auf dem Artikel „A new approach for satisfactory pensions with no guarantees“, der im Dezember letzten Jahres im European Actuarial Journal erschienen ist.

Das Rentendesign „Maximal With-Profit“

Das Rentendesign „Maximal With-Profit“ verzichtet auf Garantien und bietet stattdessen durch Korridor-Glättungsmethoden eine neue Qualität an Sicherheit. Damit werden einerseits riskantere Veranlagungsstrategien mit höheren erwarteten Renditen möglich, andererseits gelingt es mit dem Einsatz dynamischer Glättungsmethoden die Erträge gegenüber einem Absinken aus einem vordefinierten Korridor abzusichern.

Beim Rentendesign „Maximal With-Profit“ wird zwischen Ansparphase und Rentenphase unterschieden. In der Ansparphase, vom Vertragsbeginn bis zum Beginn der Rentenzahlungen, werden Beiträge des Versicherungsnehmers veranlagt. Dabei werden die Nettoprämien, nach Abzug der Kosten, zwischen einem vertragsindividuellen Konto und eine kollektiven Konto aufgeteilt. Das individuelle Konto ist einem Vertrag zugeordnet und beinhaltet sein Guthaben. Das kollektive Konto ist einem Kollektiv von Verträgen zugeordnet und dient als Puffer zur Glättung von Ertragsschwankungen in den individuellen Konten von Verträgen aus dem Kollektiv.  Das kollektive Konto kann einem Vertrag bei Rentenantritt, Tod oder Rückkauf anteilig gutgebracht werden.

Wir wollen darauf hinweisen, dass – anders als bei fondsgebundenen Versicherungen gewohnt – der einzelne Versicherungsnehmer keine Möglichkeiten hat, die Anlagestrategie mitzugestalten, vielmehr liegt die Vermögensverwaltung vollständig in den Händen des Versicherers.

Korridorglättung

Wir wenden uns der Glättung von Ertragsschwankungen in den vertragsindividuellen Konten zu. Der Einfachheit halber betrachten wir dabei ein individuelles Konto und ein kollektives Konto – klarerweise wird das kollektive Konto für die Glättung aller individueller Konten zu Verträgen im Kollektiv verwendet. Für unsere Darstellung ist es aber ausreichend, sich auf ein individuelles Konto und ein kollektives Konto zu beschränken. Wir betrachten, ebenfalls vereinfachend, einen Zeitraum ohne Ein- bzw. Auszahlungen. Das heißt ohne Prämienzahlungen und auch ohne Rentenantritt, Todesfall oder Rückkauf.

Bei der Korridorglättung wird die Entwicklung des individuellen Kontos zu diskreten Zeitpunkten, sagen wir t₀, t₁, …, t_n, … beobachtet. Liegt in t_i der Wert des individuellen Kontos K(t_i) außerhalb des Intervalls K(t_i-1) * [1 – k, 1 + k], so findet ein Ausgleich mit dem kollektiven Konto statt. Wenn das individuelle Konto einen niedrigeren Wert aufweist, K(t_i) < K(t_i-1) * (1 – k), so wird ein Anteil q des Defizits K(t_i-1) * (1 – k) – K(t_i) aus dem kollektiven Konto ausgeglichen, demgegenüber wird bei einem höheren Wert, K(t_i) > K(t_i-1) * (1 + k), ein Anteil p des Überschusses K(t_i) – K(t_i-1) * (1 + k) an das kollektive Konto transferiert.

Die Größe des Korridors ist abhängig von der Wahl des Parameters k. Wertsenkungen außerhalb des Korridors werden teilweise ausgeglichen, Wertsenkungen innerhalb des Korridors dagegen nicht. Damit kann es durch fortwährende Wertsenkungen, die innerhalb des Korridors bleiben, zu einem Abschmelzen des Guthabens im individuellen Konto kommen. Die angeführte Korridorglättung bietet dagegen keine Absicherung.

Im Folgenden illustrieren wir das Vorgehen anhand eines Beispiels.

Beispiel zur Korridorglättung

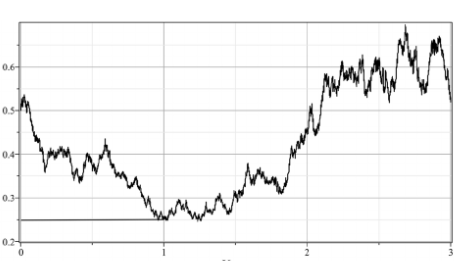
Wir legen uns auf eine jährliche Betrachtung und die Parameter k = 0.1, p = 0.25 und q = 0.5 fest und betrachten ein gegebenes Szenario für die Entwicklung des individuellen Kontos, siehe untenstehende Abbildung.

Szenario für Wertentwicklung des invidiuellen Kontos, aus Carmen Boado-Penas M. et al.

Das individuelle Konto startet mit K(0)=0.5 und liegt nach einem Jahr bei K(1)=0.25 und also außerhalb des Korridors K(0) * [1 – k, 1 + k] = 0.5 * [1 – 0.1, 1  + 0.1] = [0.45, 0.55]. Der Anteil q des Verlusts q * (K(0) * (1 – k) – K(1)) = 0.5 * (0.5 * 0.9 – 0.25) = 0.1 wird aus dem kollektiven Konto ausgeglichen. Das individuelle Konto K(1)^Neu hat nach dem Ausgleich den Wert

K(1)^Neu = K(1) + q * (K(0) * (1- k) – K(1)) = 0.25 +0.1 = 0.35

In der folgenden Abbildung ist der Zufluss in das individuelle Konto in Zeitpunkt 1 zu sehen.

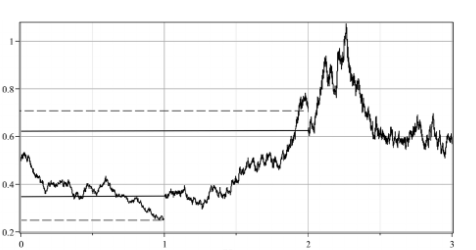
Szenario der Wertentwicklung des individuellen Kontos mit Zufluss in 1 und Abfluss in 2, aus Carmen Boado-Penas M. et al.

Wir machen eine Anmerkungen zum Vergleich der Pfade in den beiden Abbildungen. Die Pfade sind im Zeitraum [0,1) identisch, in [1,2) unterscheiden sie sich. Ein Unterschied ist der Zufluss in 1. Der Unterschied beschränkt sich aber nicht darauf, weil eine Änderung des Anfangswerts auch die Entwicklung des Prozesses verändern kann, wie dies z. B. bei einer geometrischen Brownschen Bewegung der Fall ist.

Im zweiten Jahr startet das individuelle Konto mit dem Wert K(1)^Neu = 0.35 und endet mit K(2) = 0,7. Die Wertentwicklung ist damit außerhalb des Korridors K(1)^Neu * [1 – k, 1 + k] = 0.35 * [1 – 0.1, 1  + 0.1] = [0.315, 0.385]. Der Anteil p des Überschusses p * (K(2) – K(1)^Neu * (1+k)) = 0.25 * (0.7 – 0.35 * 1.1) = 0.07875 wird an das kollektive Konto transferiert. Danach ist der Wert des individuellen Kontos K(2)^Neu gegeben durch

K(2)^Neu = K(2) – p * (K(2) – K(1)^Neu * (1+k)) = 0.7 – 0.07875 = 0.62125

Wir wollen anmerken, dass K(1)^Neu bzw. K(2)^Neu als Linearkombination zwischen K(1) bzw. K(2) und der näheren Grenze des Glättungskorridors dargestellt werden kann,

K(1)^Neu = (1 – q) * K(1) + q * K(0) * (1- k) bzw. K(2)^Neu = (1 – p) * K(2) + p * K(1)Neu * (1+k).

Im dritten Jahr startet das individuelle Konto mit dem Wert K(2)^Neu = 0.62125 und landet am Ende beim Wert K(3) = 0.6. Damit ist der Wert innerhalb des Glättungskorridors von 0.62125 * [1 + 0.1, 1 – 0.1] = [0.559125, 0.683375], es gibt keinen Ausgleich mit dem kollektiven Konto.

Die relativ hohen Werte des individuellen Kontos K(t) während des dritten Jahres werden nicht berücksichtigt, weil die Glättung jährlich angewendet wird. Klarerweise können auch kürzere Zeitintervalle für die Beobachtung der Entwicklung – und damit für einen eventuellen Ausgleich mit dem kollektiven Konto – zugrunde gelegt werden.

Interner Ausgleich

Erfolgt ein Ausgleich zwischen individuellem und kollektivem Konto in kurzen Zeitabständen, so führt dies, wenn man an Kauf und Verkauf von Wertpapieren denkt, zu hohen Transaktionskosten und Einschränkungen bezüglich der Veranlagung in langfristige oder illiquide Vermögenswerte. Deshalb ist es gewünscht, beim Ausgleich – soweit als möglich – keinen Kauf und Verkauf von Wertpapieren durchzuführen, sondern den Ausgleich intern abzuwickeln. Wenn die insgesamt vom individuellen und kollektiven Konto gehaltenen Wertpapiere oder Fondsanteile unverändert bleiben, reicht es, intern Anteile an Wertpapieren oder Fondsanteile zwischen individuellem und kollektivem Konto zu transferieren. Es ist sofort zu sehen, dass ein interner Ausgleich immer möglich ist, wenn im individuellen und im kollektiven Konto gleich veranlagt wird. Aber die Anwendung des internen Ausgleichs ist nicht darauf beschränkt.

Wir wollen ein einfaches Beispiel für die Anwendung des internen Ausgleichs geben, wenn sich die Veranlagung zwischen dem individuellen Konto und dem kollektiven Konto unterscheidet. Werde in 2 Fonds veranlagt, in einen ertrags- und risikoreicheren Fonds H₁ und einen konservativeren Fonds H₂. Sowohl das individuelle Konto als auch das kollektive Konto veranlagen in beide Fonds, aber in unterschiedlicher Aufteilung auf H₁ und H₂  – das kollektive Konto veranlagt konservativer, also stärker in Fonds H₂ als das individuelle Konto. Seien die Kurse zum Ende der betrachteten Periode H₁(t_i) und H₂(t_i) und die Anteile im individuellen Konto AH₁(t_i) und AH₂(t_i). Ist nun ein Geldbetrag G vom individuellen Konto auf das kollektive Konto zu transferieren, so können die Anteile im individuellen Konto gleichmäßig reduziert werden. Sei x durch x * ( AH₁(t_i) * H₁(t_i) + AH₂(t_i) * H₂(t_i) ) = G gegeben, so können x * AH₁(t_i) Anteile von H₁ und x * AH₂(t_i) Anteile von H₂ transferiert werden. Im Allgemeinen ändert sich die Aufteilung des Guthabens des kollektiven Kontos durch den Transfer. Analog können bei einem Transfer eines Geldbetrags vom kollektiven auf das individuelle Konto die Anteile des kollektiven Kontos gleichmäßig reduziert werden.

Was passiert, wenn das kollektive Konto leer ist?

Was passiert, wenn das kollektive Konto nicht ausreicht, die Wertsenkungen der individuellen Konten zu Verträgen im Kollektiv auszugleichen? Dazu gibt es mehrere Ansätze. Zunächst wird für diesen Fall oft ein zusätzlicher Puffer aufgebaut, der nicht aus Beiträgen der Versicherungsnehmer, sondern aus anderen Mitteln gespeist wird – beispielsweise gibt es in den Produkten zur reinen Beitragszusage einen zusätzlichen Puffer aus Arbeitgeberbeiträgen oder bei einem Produkt zur privaten Altersvorsorge einen zusätzlichen Puffer aus Eigenmitteln des Versicherungsunternehmens.

Ein anderer Ansatz besteht darin, die oben eingeführten Parameter im Korridorglättungsverfahren über die Zeit nicht zwingend konstant zu halten, sondern jährlich anzupassen. Dabei kann angestrebt werden, dass das kollektive Konto bezogen auf die Summe der Guthaben aus individuellen Konten um einen Zielwert schwankt, nicht kurzfristig, sondern über längere Zeitperioden betrachtet. Konkret kann dies analog wie bei klassischer Überschussbeteiligung durchgeführt werden. Jährlich werden die Parameter für das nachfolgende Jahr festgelegt und die Versicherungsnehmer informiert.

Zusammenfassung und Ausblick

Beim Rentendesign „Maximal With-Profit“ wird die Entwicklung der individuellen Guthaben durch Ausgleich mit dem Kollektiv geglättet. Es kommt zu einem Ausgleich über die Zeit bzw. über die Generationen von Verträgen, bei inhomogenen Verträgen kann es auch zu einem Ausgleich zwischen verschiedenen Verträgen kommen. Im Vergleich mit einer Absicherung über Finanzmarktinstrumente entstehen beim Ausgleich im Kollektiv keine zusätzlichen Kosten.

In einem weiteren Beitrag betrachten wir die Rentenbezugsphase zum Rentendesign „Maximal With-Profit“.